A través de este algoritmo podremos entender por qúe la computación cuántica puede ofrecer mejoras en el tiempo de ejecución de carácter exponencial frente a la computación clásica.

Su nombre se debe a David Deutsch, profesor de la Universidad de Oxford.

¿Y como vamos a conseguir eso objetivo?

Empecemos imaginando que tenemos una función básica, , que tiene como dominio y de igual manera tiene como imagen . Es esta una función muy básica: puede dar siempre el mismo valor, ya sea 0 ó 1, a cualquier valor de entrada, o por el contrario puede ofrecer una valor diferente segun sea el valor de x. Llamaremos constantes al primer tipo de función, y balanceadas al segundo.

El problema al que nos enfrentamos se reduce a averiguar, dada una función , de que tipo es.

Si disponemos de un ordenador clásico: ¿cuantas llamadas a la función hemos de hacer?. Es clara la respuesta : 2 veces.

Duetsch nos mostró que con un ordenador, o circuito, cuántico basta con hacer una sola llamada.

Veámoslo….

Partimos con un circuito cuántico tal cual mostramos en la figura 1.

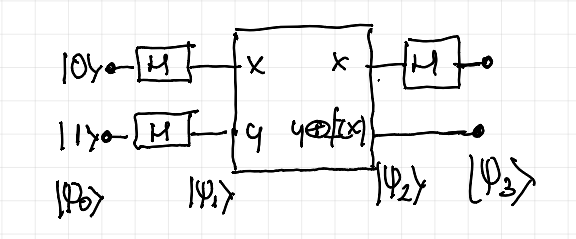
Tenemos aquí un circuito con dos qubits , el primero de los cuales llamaremos qubit de entrada, inicializado a y qubit de referencia al segundo, inicializado a , y dos qubits de salida, siendo uno de ellos el que nos indica el resultado del algortimo. A los dos primeros se les aplica una puerta de Hadamard, que ya hemos estudiado en una entrada anterior y que básicamente aplica una superposición al qubit correspondiente. El circuito en sí, que denominamos aplica al segundo quibit una suma exclusica, , entre el qubit de control y el resultado de aplicar la función al qubit de entrada.

Entremos en el detalle, calculando cada unos de los 4 estados que hemos llamado .

El primero es inmediato, pues se refiere a los qubits inicializados. Luego . Recordemos que utilizamos la convención de indicar a la izquierda el qubit con la posición superior.

Tras aplicar la puerta Hadamard a los dos qubits nos encontramos con :

vemos como la puerta de Hadamard provoca el paralelismo, al convertir un quibit de valor 0 ó 1 en una superposición.

Pasamos a calcular , para ello vamos a calcular de manera genérica , que equivale a dejar el primer termino tal cual y aplicar la suma exclusiva al segundo término y para continuar vamos a considerar dos escenarios separados :

si

• si
• si

Luego podemos simplificar agrupando los dos términos tal que

Estos calculos previos nos permiten avanzar con el cálculo de :

, que de igual manera que en el paso previo vamos a dividir en varios escenarios, tal que :

que se puede simplificar tal que :

Finalmente aplicamos la puerta de Hadamard de salida al primer qubit , y tendremos :

…que a su vez podemos simplificar :

¿Y que nos indica esa expresión?: que podemos medir el primer qubit de ese estado cuántico resultante, si es cero sabremos que la función es constante, y balanceada si el valor es 1.

Con un solo ciclo de ejecución de llamada a la función, con el estado de dos qubits , podremos averiguarde que tipo es, ofreciendo por tanto una gran ventaja en complejidad de computación sobre un ordenador de computación clásica que necesitará dos llamadas.

Este algoritmo se puede extender a funciones de manera que veremos en una siguiente entrada en el blog.

He preparado este trabajo leyendo el capítulo 1.4.3 del libro Quantum Computation and Quantum Informacion de Michael A. Nielsen & Isaac L. Chuang y el capítulo 7.2 del Introduction to Classical and Quantum Computing de Thomas G. Wong ,