Autor: Manuel H. Arias

Trabajo en el sector tecnológico. En mi tiempo libre aprendo IA, machine learning, como obtener información de las fuentes OpenData con Python, QC..always learning..

Distribución Cuántica de Claves: Protocolo BB84

Manuel H. AriasDeja un comentario

Objetivo

La Distribución Cuántica de Claves (QKD : Quantum Key Distribution) es un método por el que dos partes, que comparten un canal de comunicación no seguro pueden construir, negociar y acordar una clave secreta.

En este artículo vamos a analizar este procedimiento, sin entrar en la propia generación de la clave.

Describiremos como funciona el protocolo BB84, desarrollado por Charles Bennett y Gilles Brassard en 1984.

Leer más »

Algoritmo de Deutsch

Manuel H. AriasDeja un comentario

A través de este algoritmo podremos entender por qúe la computación cuántica puede ofrecer mejoras en el tiempo de ejecución de carácter exponencial frente a la computación clásica.

Su nombre se debe a David Deutsch, profesor de la Universidad de Oxford.

¿Y como vamos a conseguir eso objetivo?

Empecemos imaginando que tenemos una función básica, f , que tiene como dominio Dom f = \{0,1\} y de igual manera tiene como imagen Im f = \{0,1\} . Es esta una función muy básica: puede dar siempre el mismo valor, ya sea 0 ó 1, a cualquier valor de entrada, o por el contrario puede ofrecer una valor diferente segun sea el valor de x. Llamaremos constantes al primer tipo de función, y balanceadas al segundo.

El problema al que nos enfrentamos se reduce a averiguar, dada una función f, de que tipo es.

Si disponemos de un ordenador clásico: ¿cuantas llamadas a la función hemos de hacer?. Es clara la respuesta : 2 veces.

Duetsch nos mostró que con un ordenador, o circuito, cuántico basta con hacer una sola llamada.

Veámoslo….

Partimos con un circuito cuántico tal cual mostramos en la figura 1.

Figura 1: esquema del circuito cuántico necesario para el Algoritmo de Deutsch

Tenemos aquí un circuito con dos qubits , el primero de los cuales llamaremos qubit de entrada, inicializado a |0\rangle y qubit de referencia al segundo, inicializado a |1\rangle , y dos qubits de salida, siendo uno de ellos el que nos indica el resultado del algortimo. A los dos primeros se les aplica una puerta de Hadamard, que ya hemos estudiado en una entrada anterior y que básicamente aplica una superposición al qubit correspondiente. El circuito en sí, que denominamos U_{f} aplica al segundo quibit una suma exclusica, XOR, entre el qubit de control y el resultado de aplicar la función f al qubit de entrada.

Entremos en el detalle, calculando cada unos de los 4 estados que hemos llamado \psi_{0} ,\psi_{1}, \psi_{2} \ y\ \psi_{3} .

El primero es inmediato, pues se refiere a los qubits inicializados. Luego \psi_{0} = |01\rangle. Recordemos que utilizamos la convención de indicar a la izquierda el qubit con la posición superior.

Tras aplicar la puerta Hadamard a los dos qubits nos encontramos con :

|\psi_{1}\rangle = H^{\otimes 2} |01\rangle = \left (\frac {|0\rangle + |1\rangle}{\sqrt{2}} \right ) \left (\frac {|0\rangle - |1\rangle}{\sqrt{2}} \right ) vemos como la puerta de Hadamard provoca el paralelismo, al convertir un quibit de valor 0 ó 1 en una superposición.

Pasamos a calcular \psi_{2}, para ello vamos a calcular de manera genérica U_{f} |x\rangle \left (\frac {|0\rangle - |1\rangle}{\sqrt{2}} \right ) , que equivale a dejar el primer termino tal cual y aplicar la suma exclusiva al segundo término U_{f} |x \rangle \left (\frac {|0\rangle - |1\rangle}{\sqrt{2}} \right ) = |x \rangle \left (\frac {|0\oplus{f(x)}\rangle - |1\oplus{f(x)}\rangle}{\sqrt{2}} \right ) y para continuar vamos a considerar dos escenarios separados :

si

  • si f(x)=0 \rightarrow |x\rangle \left (\frac {|0\oplus{f(x)}\rangle - |1\oplus{f(x)}\rangle}{\sqrt{2}} \right ) = |x\rangle \left (\frac {|0\rangle - |1\rangle}{\sqrt{2}} \right )
  • si f(x)=1 \rightarrow |x\rangle \left (\frac {|0\oplus{f(x)}\rangle - |1\oplus{f(x)}\rangle}{\sqrt{2}} \right ) = |x\rangle \left (\frac {|1\rangle - |0\rangle}{\sqrt{2}} \right )

Luego podemos simplificar agrupando los dos términos tal que (-1)^{f(x)} |x\rangle \left (\frac {|0\rangle - |1\rangle}{\sqrt{2}} \right )

Estos calculos previos nos permiten avanzar con el cálculo de \psi_{2} :

\psi_{2}= \frac {\left ((-1)^{f(0)}|0\rangle + (-1)^{f(1)}|1\rangle \right )}{\sqrt{2}} \left ( \frac { |0\rangle - |1\rangle }{\sqrt{2}} \right ), que de igual manera que en el paso previo vamos a dividir en varios escenarios, tal que :

|\psi_{2} \rangle = \left\{ \begin{aligned} & +\left ( \frac {\left (|0\rangle + |1\rangle \right )}{\sqrt{2}} \right ) \left ( \frac { |0\rangle - |1\rangle }{\sqrt{2}} \right ) \quad si f(0)=f(1)=0 \\ & - \left ( \frac {\left (|0\rangle + |1\rangle \right )}{\sqrt{2}} \right ) \left ( \frac { |0\rangle - |1\rangle }{\sqrt{2}} \right ) \quad si f(0)=f(1)=1 \\ & + \left ( \frac {\left (|0\rangle - |1\rangle \right )}{\sqrt{2}} \right ) \left ( \frac { |0\rangle - |1\rangle }{\sqrt{2}} \right ) \quad si f(0)=0 \ y \ f(1)=1 \\ & - \left (\frac {\left (|0\rangle - |1\rangle \right )}{\sqrt{2}} \right ) \left ( \frac { |0\rangle - |1\rangle }{\sqrt{2}} \right ) \quad si f(0)=1 \ y \ f(1)=0 \end{aligned} \right.

que se puede simplificar tal que :

|\psi_{2} \rangle = \left\{ \begin{aligned} & \pm \left ( \frac {\left (|0\rangle + |1\rangle \right )}{\sqrt{2}} \right ) \left ( \frac { |0\rangle - |1\rangle }{\sqrt{2}} \right ) \quad si f(0)=f(1) \\ & \pm \left ( \frac {\left (|0\rangle - |1\rangle \right )}{\sqrt{2}} \right ) \left ( \frac { |0\rangle - |1\rangle }{\sqrt{2}} \right ) \quad si f(0) \neq f(1) \end{aligned} \right.

Finalmente aplicamos la puerta de Hadamard de salida al primer qubit , y tendremos :

|\psi_{3} \rangle = \left\{ \begin{aligned} & \pm |0\rangle \left ( \frac { |0\rangle - |1\rangle }{\sqrt{2}} \right ) \quad si f(0)=f(1) \\ & \pm |1\rangle \left ( \frac { |0\rangle - |1\rangle }{\sqrt{2}} \right ) \quad si f(0) \neq f(1) \end{aligned} \right.

…que a su vez podemos simplificar :

\psi_{3} = \pm | f(0) \oplus f(1) \rangle \left ( \frac {|0\rangle - |1\rangle}{\sqrt{2}} \right )

¿Y que nos indica esa expresión?: que podemos medir el primer qubit de ese estado cuántico resultante, si es cero sabremos que la función es constante, y balanceada si el valor es 1.

Con un solo ciclo de ejecución de llamada a la función, con el estado de dos qubits |01 \rangle, podremos averiguarde que tipo es, ofreciendo por tanto una gran ventaja en complejidad de computación sobre un ordenador de computación clásica que necesitará dos llamadas.

Este algoritmo se puede extender a funciones de manera Dom f = \{0,1\}^{n} que veremos en una siguiente entrada en el blog.

He preparado este trabajo leyendo el capítulo 1.4.3 del libro Quantum Computation and Quantum Informacion de Michael A. Nielsen & Isaac L. Chuang y el capítulo 7.2 del Introduction to Classical and Quantum Computing de Thomas G. Wong ,

La puerta de Hadamard

Manuel H. Arias1 comentario

¿Qué es una puerta Hadamard?

La puerta de Hadamard es un operador de computación cuántica, muy simple a la vez que, probablemente, de los más usados. Su utilidad reside en su capacidad de convertir un qubit de un estado, tal que |0\rangle o |1\rangle, en una superposición de los mismos. Veamos los detalles.

La puerta de Hadamard se nombra con H y se define de forma matricial tal que H= \dfrac{1}{ \sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}

\huge { \text {Puerta de Hadamard } H= \dfrac{1}{ \sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} }

Y efectivamente, si aplicamos una puerta Hadamard a |0\rangle queda tal que:

\dfrac{1}{ \sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} |0\rangle = \dfrac{1}{ \sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \dfrac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ 1 \end{pmatrix} = \dfrac{1}{ \sqrt{2}} (|0\rangle + |1\rangle)

…de igual manera si aplicamos Hadamard a un qubit |1\rangle tendremos:

\dfrac{1}{ \sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} |1\rangle = \dfrac{1}{ \sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \begin{pmatrix} 0 \\ 1 \end{pmatrix} = \dfrac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ -1 \end{pmatrix} = \dfrac{1}{ \sqrt{2}} (|0\rangle - |1\rangle)

Apliquemos Hadamard sobre estados en otras bases:

H |+\rangle = \dfrac{1}{ \sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} \dfrac{1}{ \sqrt{2}} (|0\rangle + |1\rangle) = \dfrac{1}{2} \begin{pmatrix} 2 \\ 0 \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} = |0\rangle

como no podía ser de otra manera, ya que H es unitaria y reversible.

Es muy útil hacer una pequeña transformación y escribir H de manera genérica para un x \in \{0,1\} tal que H|x\rangle = \dfrac {1}{\sqrt{2}} \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} |x\rangle = \dfrac{1}{\sqrt{2}}(|0\rangle + (-1)^{x}|1\rangle) , efectivamente

H|x\rangle = \dfrac{1}{\sqrt{2}}(|0\rangle + (-1)^{x}|1\rangle) = \left\{ \begin{aligned} & \text{si x=0 } H|0\rangle = \dfrac{1}{\sqrt{2}}(|0\rangle + |1\rangle) \\ & \text{si x=1 } H|1\rangle = \dfrac{1}{\sqrt{2}}(|0\rangle - |1\rangle) \end{aligned} \right.

y podemos ir un paso más allá y escribir la expresión tal que :

H |x \rangle = \dfrac{1}{\sqrt{2}}\left(|0\rangle + (-1)^{x}|1\rangle\right) = \dfrac{1}{\sqrt{2}} \left(\sum\limits_{y=0}^{1}(-1)^{xy}|y\rangle\right) \text{para } x\in \{0,1\}

Hadamard sobre multiples qubits..

Hadamard es una puerta que opera sobre un sólo qubit, pero en circuitos multiqubits no es infrecuente aplicar simultáneamente esta puerta sobre todos los qubits. En algunos textos se le denomina tensor Hadamard o H^{\otimes n} . Hagamos un caso práctico de aplicación de este tensor a un estado cuántico genérico | \psi \rangle = |x_{1} x_{2}x_{3}..x_{n}\rangle con x_{i} \in \{0,1\} \forall i \in \{1,2..,n\}

H^{\otimes n}| \psi \rangle = H^{\otimes n} |x_{1} x_{2}x_{3}..x_{n}\rangle = H |x_{1}\rangle \otimes H |x_{2} \rangle \otimes H |x_{3} \rangle \otimes ..H|x_{n}\rangle

..es importante ver que se está aplicando una puerta a cada uno de los estados simples y multiplicando tensorialmento esos n resultados. Utilizando la expresión genérica que usamos en el apartado anterior podemos continuar con:

H |x_{1} \rangle \otimes H |x_{2}\rangle \otimes H |x_{3}\rangle \otimes \cdots H|x_{n}\rangle = \dfrac{1}{\sqrt{2}}(|0\rangle + (-1)^{x_{1}}|1\rangle) \otimes \dfrac{1}{\sqrt{2}}(|0\rangle + (-1)^{x_{2}}|1\rangle)\cdots\otimes \dfrac{1}{\sqrt{2}}(|0\rangle + (-1)^{x_{n}}|1\rangle) = \dfrac{1}{\sqrt{2}}\left(\sum\limits_{y_{1}=0}^{1}(-1)^{x_{1}y_{1}}|y_{1}\rangle\right) \otimes \left(\sum\limits_{y_{2}=0}^{1}(-1)^{x_{1}y_{2}}|y_{2}\rangle\right) \cdots \otimes \left(\sum\limits_{y_{n}=0}^{1}(-1)^{x_{n}y_{n}}|y_{n}\rangle\right)

..que se puede simplificar con \dfrac{1}{\sqrt{2^{n}}} \sum\limits_{y\in\{0,1\}^{n}}(-1)^{x_{1}y_{1}+x_{2}y_{2}\cdots x_{n}y_{n}}|y\rangle = \dfrac{1}{\sqrt{2^{n}}} \left(\sum\limits_{y\in\{0,1\}^{n}}(-1)^{\sum\limits_{i=1}^{n}x_{i}y_{i}}|y\rangle \right)

La manera intuitiva de llegar a esta última expresión es viendo como cada componente |0\rangle de cuaquier estado de múltiples qubits lleva siempre signo positivo, ya que todo producto x_iy_i con x_i=0 será cero, y el componte |1\rangle lleva un signo tal que (-1)^{x_{i}} , que se suman para el estado final de multiples qubits.

Veamos un caso particular con n=3..

H^{\otimes n}| \psi \rangle = H^{\otimes 3} |x_{1} x_{2}x_{3} \rangle= H |x_{1}\rangle \otimes H |x_{2} \rangle \otimes H |x_{3} \rangle = \dfrac{1}{ \sqrt{2^{3}}} \left ( \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} |x_{1} \rangle \otimes \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} |x_{2} \rangle \otimes \begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix} |x_{3} \rangle \right) = \dfrac{1}{ \sqrt{2^{3}}} \bigg ( \Big ((-1)^{x_{1}*0}|0\rangle + (-1)^{x_{1}*1}|1\rangle \Big ) \Big ((-1)^{x_{2}*0}|0\rangle + (-1)^{x_{2}*1}|1\rangle \Big ) \Big ((-1)^{x_{3}*0}|0\rangle + (-1)^{x_{3}*1}|1\rangle \Big ) \bigg ) = \dfrac{1}{ \sqrt{2^{3}}} \Big ( (-1)^{(x_{1}*0+x_{2}*0+x_{3}*0)} |000\rangle + (-1)^{(x_{1}*0+x_{2}*0+x_{3}*1)} |001\rangle + (-1)^{(x_{1}*0+x_{2}*1+x_{3}*0)} |010\rangle + (-1)^{(x_{1}*0+x_{2}*1+x_{3}*1)} |011\rangle + (-1)^{(x_{1}*1+x_{2}*0+x_{3}*0)} |100\rangle + (-1)^{(x_{1}*1+x_{2}*0+x_{3}*1)} |101\rangle + (-1)^{(x_{1}*1+x_{2}*1+x_{3}*0)} |110\rangle + (-1)^{(x_{1}*1+x_{2}*1+x_{3}*1)} |111\rangle \Big ) = \dfrac{1}{ \sqrt{2^{3}}} \Big (|000\rangle + (-1)^{(x_{3})} |001\rangle + (-1)^{(x_{2})} |010\rangle + (-1)^{(x_{2}+x_{3})} |011\rangle + (-1)^{(x_{1})} |100\rangle +(-1)^{(x_{1}+x_{3})} |101\rangle + (-1)^{(x_{1}+x_{2})} |110\rangle + (-1)^{(x_{1}+x_{2}+x_{3})} |111\rangle \Big )

Hemos visto la definición de la puerta de Hadamard, su utilidad para provocar una superposición desde un estado de una sola base, y hemos trabajado un poco de álgebra para generar una expresión genérica del tensor Hadamard sobre múltiples qubits, que será muy útil en la demostración del algoritmo de Deutsch-Jozsa que veremos más adelante.

Por cierto, esta puerta debe su nombre al matemático francés Jacques Hadamard.

Tratando de entender la Física Cuántica: Principio de No Clonación

Manuel H. AriasDeja un comentario

Uno de los pilares sobre los que se apoya la física cuántica es el principio de no clonación o no replicabilidad.

¿Qué significa eso?: que no podemos copiar el estado de un qubit, o dicho de otra manera que no podemos replicar su estado cuántico en otro qubit. Copiar bits en la computación «clásica» es una operación más que cotidiana, forma parte intrínseca de las operaciones, y no nos podemos imaginar un escenario en el que no podamos hacerlo.

«The no-cloning theorem is one of the key results in quantum mechanics that reflects the underlying non-classical nature of quantum information.»

Fuente: Deutsch, D., Ekert, A., & Jozsa, R. (1996). Quantum privacy amplification and the security of quantum cryptography over noisy channels. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 452(1954), 1799-1824.

¿Y como podemos demostrar una cosa así?, pues con un poquito de álgebra, espacios vectoriales y productos escalares.

Vamos a ello1…

En primer lugar pensaremos en un operador lineal U aplicable a dos qubits tal que replica el valor de uno de ellos en el otro. Lo podemos expresar en lenguaje matemático tal que :

U|\phi 0\rangle = | \phi \phi \rangle

que indica que aplicamos el operador sobre |\phi \phi \rangle y obtenemos un par de qubits iguales. Habríamos replicado \phi en el qubit con valor inicial 0 . La dimensión del operador U es 4×4, ya que aplica a dos qubits.

Podemos desarrollar el término de la izquierda tal que :

\begin{pmatrix} u_{11} & u_{12} & u_{13} & u_{14} \\ u_{21} & u_{22} & u_{23} & u_{24} \\ u_{31} & u_{32} & u_{33} & u_{34} \\ u_{41} & u_{42} & u_{43} & u_{44} \end{pmatrix} \begin{pmatrix} \alpha \\ \beta \end{pmatrix} \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix} = \begin{pmatrix} u_{11} & u_{12} & u_{13} & u_{14} \\ u_{21} & u_{22} & u_{23} & u_{24} \\ u_{31} & u_{32} & u_{33} & u_{34} \\ u_{41} & u_{42} & u_{43} & u_{44} \end{pmatrix} \begin{pmatrix} \alpha \begin{pmatrix} 1 \\ 0 \end{pmatrix} \\ \beta \begin{pmatrix} 1 \\ 0 \end{pmatrix} \end{pmatrix} = \begin{pmatrix} u_{11} & u_{12} & u_{13} & u_{14} \\ u_{21} & u_{22} & u_{23} & u_{24} \\ u_{31} & u_{32} & u_{33} & u_{34} \\ u_{41} & u_{42} & u_{43} & u_{44} \end{pmatrix} \begin{pmatrix} \alpha \\ 0 \\ \beta \\ 0 \end{pmatrix} = \begin{pmatrix} u_{11} \alpha + u_{13} \beta \\ u_{21} \alpha + u_{23} \beta \\ u_{31} \alpha + u_{33} \beta \\ u_{41} \alpha + u_{43} \beta \end{pmatrix}

y si desarrollamos el término de la derecha:

| \phi \phi \rangle = \begin{pmatrix} \alpha \\ \beta \end{pmatrix} \otimes \begin{pmatrix} \alpha \\ \beta \end{pmatrix} = \begin{pmatrix} \alpha \begin{pmatrix} \alpha \\ \beta \end{pmatrix} \\ \beta \begin{pmatrix} \alpha \\ \beta \end{pmatrix} \end{pmatrix} = \begin{pmatrix} \alpha^2 \\ \alpha \beta \\ \alpha \beta \\ \beta^2 \end{pmatrix}

Igualando ambas expresiones obtenemos estas cuatro ecuaciones :

u_{11} \alpha + u_{13} \beta = \alpha^2

u_{21} \alpha + u_{23} \beta = \alpha \beta

u_{31} \alpha + u_{33} \beta = \alpha \beta

u_{41} \alpha + u_{43} \beta = \beta^2

de aquí podemos conseguir muchas soluciones, pero que siempre serán función de \alpha y \beta . Sólo como ejemplo :

u_{11}=\alpha , u_{13} = 0 , u_{21} = 0 , u_{23} = \alpha , u_{31} = \beta , u_{33} = 0 , u_{41} = 0 , u_{43} = \beta

Podemos observar como la matriz U tiene componentes función del qubit a replicar, luego no existe un operador U que replique el estado cuántico de un qubit en otro.

  1. Demostración extraída del libro Introduction to Classical and Quantum Computing de Thomas G. Wong. Capítulo 4.4.4 No-Cloning Theorem ↩︎

Resumen de puertas y qubits comunes en quantum computing

Manuel H. AriasDeja un comentario

Me he preparado esta tabla con la definición de las puertas y qubits más frecuentes. Iré actualizanda conforme avanzo en el estudio de esta teoría.

IdentityI|0\rangle = |0\rangle
I|1\rangle = |1\rangle 		I = \begin{pmatrix}1&0\\0&1\end{pmatrix}
Pauli XX|j\rangle = |1 \oplus j\rangle \; \text{para j=\{0,1\}}
X|0\rangle = |1 \rangle
X|1\rangle = |0\rangle 		X = \begin{pmatrix}0&1\\1&0\end{pmatrix}
Pauli YY|j\rangle = (-i)^{j}|1\oplus j\rangle \; \text{para j=\{0,1\}}
Y|0\rangle = i|0\rangle
Y|1\rangle = -i|1\rangle 		Y = \begin{pmatrix}0&{-i}\\{i}&0\end{pmatrix}
Pauli ZZ|j\rangle = (-1)^j |j\rangle \; \text{para j=\{0,1\}}
Z|0\rangle = |0\rangle
Z|1\rangle = -|1\rangle 		Z = \begin{pmatrix}1&0\\0&-1\end{pmatrix}
Phase SS|0\rangle = |0\rangle
S|1\rangle = i|1\rangle 		S = \begin{pmatrix}1&0\\0&i\end{pmatrix}
TT|0\rangle = |0\rangle
T|1\rangle = e^{i\frac{\pi}{4}}|1\rangle 		T = \begin{pmatrix}1&0\\0&e^{i\frac{\pi}{4}}\end{pmatrix}
H
Hadamard		H|0\rangle = \frac{1}{\sqrt{2}}\left(|0\rangle+|1\rangle\right)
H|1\rangle = \frac{1}{\sqrt{2}}\left(|0\rangle-|1\rangle\right) 		H = \frac{1}{\sqrt{2}}\begin{pmatrix}1&1\\1&-1\end{pmatrix}
|+\rangle
|-\rangle 		|+\rangle = \frac{1}{\sqrt{2}}\left(|0\rangle+|1\rangle\right)
|-\rangle = \frac{1}{\sqrt{2}}\left(|0\rangle-|1\rangle\right)
|i\rangle
|-i\rangle 		|i\rangle = \frac{1}{\sqrt{2}}\left(|0\rangle+i|1\rangle\right)
|-i\rangle = \frac{1}{\sqrt{2}}\left(|0\rangle-i|1\rangle\right)
|\phi^{+}\rangle
|\phi^{-}\rangle
|\phi^{+}\rangle = \frac{1}{\sqrt{2}}\left(|00\rangle+|11\rangle\right)
|\phi^{-}\rangle = \frac{1}{\sqrt{2}}\left(|00\rangle-|11\rangle\right)
|\psi^{+}\rangle
|\psi^{-}\rangle 		|\psi^{+}\rangle = \frac{1}{\sqrt{2}}\left(|01\rangle+|10\rangle\right)
|\psi^{-}\rangle = \frac{1}{\sqrt{2}}\left(|01\rangle-|10\rangle\right)

Trabajando con Datetime y Time

Manuel H. AriasDeja un comentario
Photo by Pixabay on Pexels.com

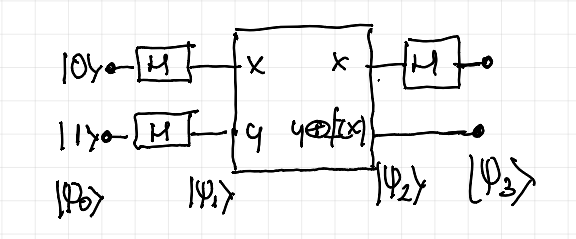
Comenzamos…

Dejamos ya importadas las librerías que vamos a necesitar:

import datetime
import time
import numpy as np
from datetime import datetime,timedelta
from zoneinfo import ZoneInfo, available_timezones
import calendar
%matplotlib inline
import pandas as pd
import sys

A raiz de la actualización del código que soporta al @elgalloaurora he estado jugando y probando con el tratamiento y gestión de horas con sus diferentes versiones “naive” y “no naive” y el cambio entre UTC, referenciadas a diferentes timezones y en modo segundos desde un determinado epoch. He escrito este pqueño doc para que me sirva de memoria para futuros trabajos

Vemos cosas básicas, como :

Horal actual local

datetime.now(ZoneInfo('Europe/Madrid'))

datetime.datetime(2024, 5, 26, 11, 50, 47, 425942, tzinfo=zoneinfo.ZoneInfo(key='Europe/Madrid'))

datetime.now(ZoneInfo('US/Hawaii'))

datetime.datetime(2024, 5, 25, 23, 50, 47, 666428, tzinfo=zoneinfo.ZoneInfo(key='US/Hawaii'))

y aquí se puede encontrar todas las zonas disponibles:

available_timezones()

{'Africa/Abidjan',
 'Africa/Accra',
 'Africa/Addis_Ababa',
 'Africa/Algiers',
 'Africa/Asmara',
 'Africa/Asmera',
 'Africa/Bamako',
 'Africa/Bangui',
 'Africa/Banjul',
 'Africa/Bissau',
 'Africa/Blantyre',
 'Africa/Brazzaville',
 'Africa/Bujumbura',
 'Africa/Cairo',
 'Africa/Casablanca',
 'Africa/Ceuta',
 'Africa/Conakry',
 .....
 'US/Samoa',
 'UTC',
 'Universal',
 'W-SU',
 'WET',
 'Zulu',
 'build/etc/localtime'}

Otra manera de conseguir la hora actual en otra zona horaría es con astimezone

datetime.now(ZoneInfo('Europe/Madrid')).astimezone(ZoneInfo('Europe/Lisbon'))

datetime.datetime(2024, 5, 26, 10, 50, 49, 27417, tzinfo=zoneinfo.ZoneInfo(key='Europe/Lisbon'))

o directamente:

datetime.now().astimezone(ZoneInfo('Europe/Lisbon'))

datetime.datetime(2024, 5, 26, 10, 50, 49, 474078, tzinfo=zoneinfo.ZoneInfo(key='Europe/Lisbon'))

Como caso especial tenemos la hora UTC, muy útil pues es la que nos devuelven, y aceptan, muchas librerías:

datetime.now(ZoneInfo('UTC'))

datetime.datetime(2024, 5, 26, 9, 50, 50, 453552, tzinfo=zoneinfo.ZoneInfo(key='UTC'))

Hora naive y no naive:

fecha = datetime(year=2024,month=5,day=1,hour=10,minute=10)

Esa hora no tiene asociao ningún timezone, y lo podemos confirmar llamando a la función tzinfo:

fecha.tzinfo

Sin embargo esta fecha sí está asociada, en particular a Lisboa:

fecha_lisboa = datetime(year=2024,month=5,day=1,hour=10,minute=10,tzinfo=ZoneInfo(key='Europe/Lisbon'))

en efecto:

fecha_lisboa.tzinfo

zoneinfo.ZoneInfo(key='Europe/Lisbon')

Y que impacto tiene esa diferencia?: por ejemplo, que no puedes restarlas. No puedes calcular la diferencia en tiempo entre una fecha naive y no naive

fecha-fecha_lisboa

---------------------------------------------------------------------------

TypeError                                 Traceback (most recent call last)

Cell In[114], line 1
----> 1 fecha-fecha_lisboa


TypeError: can't subtract offset-naive and offset-aware datetimes

Sin embargo esto si funciona al estar comparando dos naives :

fecha_1 = datetime(year=2024,month=5,day=1,hour=10,minute=10,tzinfo= ZoneInfo('Europe/Lisbon'))

fecha_2 = datetime(year=2024,month=5,day=1,hour=11,minute=10,tzinfo= ZoneInfo('Europe/Madrid'))

qué resultado dará la resta anterior?

(fecha_1-fecha_2).seconds

0

efectivamente, la 11:10 hora local en Madrid corresponden con las 11:10 en Lisboa

Horas medidas en segundos

Este resultado nos da los segundos desde un epoch en particular. Y qué es eso de un epoch?..es una referencia, tal como se define en la documentacion oficial de la librería time : > The epoch is the point where the time starts, the return value of time.gmtime(0). It is January 1, 1970, 00:00:00 (UTC) on all platforms.

time.time()

1716717063.091218

y como conseguimos esa referencia?. La conseguimos con la ordent:

time.gmtime(0)

time.struct_time(tm_year=1970, tm_mon=1, tm_mday=1, tm_hour=0, tm_min=0, tm_sec=0, tm_wday=3, tm_yday=1, tm_isdst=0)

que podemos convertir a formato ´datetime`

datetime.fromtimestamp(time.mktime(time.gmtime(0)))

datetime.datetime(1970, 1, 1, 0, 0)

ese time.time() nos da un resultado en hora UTC. Para comprobarlo vamos a usar la función gmtime

time.gmtime(time.time())

time.struct_time(tm_year=2024, tm_mon=5, tm_mday=26, tm_hour=9, tm_min=51, tm_sec=5, tm_wday=6, tm_yday=147, tm_isdst=0)

y para conseguirla en hora actual:

time.localtime(time.time())

time.struct_time(tm_year=2024, tm_mon=5, tm_mday=26, tm_hour=11, tm_min=51, tm_sec=5, tm_wday=6, tm_yday=147, tm_isdst=1)

Y podemos conseguir esa hora en formato datetime tal como lo veíamos anteriormente

datetime.fromtimestamp(time.time()) #ojo...en local, aunque no naive

datetime.datetime(2024, 5, 26, 11, 51, 7, 303250)

datetime.fromtimestamp(time.time()).replace(tzinfo=ZoneInfo('Europe/Madrid'))

datetime.datetime(2024, 5, 26, 11, 51, 7, 536789, tzinfo=zoneinfo.ZoneInfo(key='Europe/Madrid'))

ojo, que replace tan solo cambia la timezone pero no recalcula la hora de acuerdo a ese cambio.

datetime.fromtimestamp(time.time()).replace(tzinfo=ZoneInfo('Europe/Madrid')).replace(tzinfo=ZoneInfo('Europe/Lisbon'))

datetime.datetime(2024, 5, 26, 11, 51, 7, 950463, tzinfo=zoneinfo.ZoneInfo(key='Europe/Lisbon'))

y para generar una hora en segundos desde una estructurada:

time.time()

1716717068.888389

time.gmtime(time.time())

time.struct_time(tm_year=2024, tm_mon=5, tm_mday=26, tm_hour=9, tm_min=51, tm_sec=9, tm_wday=6, tm_yday=147, tm_isdst=0)

calendar.timegm(time.gmtime(time.time()))

1716717069

que es dentro de una hora (los 3600 segundos sumados)

Y para pasar a un formato no naive desde segundos:

datetime.fromtimestamp(time.time()+3600,tz=ZoneInfo('Europe/Madrid'))

datetime.datetime(2024, 5, 26, 12, 51, 10, 228910, tzinfo=zoneinfo.ZoneInfo(key='Europe/Madrid'))

datetime.fromtimestamp(time.time(),tz=ZoneInfo('Europe/Lisbon'))

datetime.datetime(2024, 5, 26, 10, 51, 10, 435502, tzinfo=zoneinfo.ZoneInfo(key='Europe/Lisbon'))

Así como resumen, y replicando el cuadro de la documentación de la librería:

  • Cambio de segundos desde epoch a struc_time en UTC : gmtime()

  • Cambio de segundos desde epoch a struct_time en LocatTime : localtime()

  • Cambio de struct_time en UTC a segundos : calendar.timegm()

  • Cambio de struct_time local time a segundos: mktime()

    y añado dos más:

  • Cambo de datetime a time_struct : datetime.timetuple()

  • Cambio de time_struct a datetime : datetime.fromtimestamp(mktime(time_struc))

¿Cómo tuitear desde Python?

Manuel H. AriasDeja un comentario

¿Para que vale eso?

Desde mi cuenta de twitter @walyt publico diariamente diversos gráficos con información relevante del Mercado Eléctrico: precios del spot del día, como se comporta la generación, evolución precios, previsiones energía solar etc…Estos tuits los publico de manera «automatizada» por medio de scripts en Python residentes en una máquina virtual en Google Cloud. Por medio de un crontab planifico a lo largo del día esa publicación de información. Así aseguras una publicación de manera regular, y que la información de base está siempre disponible.

Me di cuenta el fin de semana pasado de que hacía varios días que no salía ningun nuevo tuit. Alarma!. Tras chequear y cacharrear un poco me di cuenta del algún cambio en la API de twitter, que hacía que el procedimiento que estaba usando no era válido. Hasta este fin de semana no he tenido unas horas para arreglarlo. Y parece que ya lo tengo. Para ayudar a quien le pase algo parecido o para quien necesite este código he preparado este post.

Qué necesito?

Lo primero que se necesita es obvio: una cuenta de twitter!!!

Venga, que me imagino que la tenéis. Lo segundo es dar de alta esa cuenta en el portal de desarrollo. Nos encontramos aquí tres modalidades :

  • Free: que te permite acceso gratuito, aunque con alguna limitación, a las APIs de Twitter. Te permite publicar hasta 1.500 tuits al mes, y realizar 50 llamadas (queries) al día. Esta es la modalidad con la que estoy subscrito.
  • Basic : con un coste de 100$/mes, dos entornos de aplicación, descarga de 10.000 tuis al mes, 1.667 peticiones cada 24 horas…
  • Pro : con un coste de 5.000€/mes se multiplican, obviamente, las capacidades: 3 entornos de aplicaciones, puedes descargar hasta un millón de tuits al mes, publicar 100 tuits cada 15 min ó 10.000 al mes. Además de muchos endpoints para la gestión total de una cuenta

…y dar de alta la APP

A continuación daremos de alta la entorno y una aplicación, simplemente hay que añadir una breve descripción…Así me aparece:

y solo queda ir a la pestaña de «Keys and tokens», en la que deberemos generar cinco claves:

  • Bearer Token que identifica a la App
  • API Key y API Secret, que tal como indica : «Think of these as the user name and password that represents your App when making API requests. While your Secret will remain permanently hidden, you can always view the last 6 characters of your API Key.»
  • Access Token and Access Secret, que de igaul manera describe como : «An Access Token and Secret are user-specific credentials used to authenticate OAuth 1.0a API requests. They specify the Twitter account the request is made on behalf of.«

copia, de manera segura, esas claves y ya estaríamos listos para empezar con Python

Un poco de código 

#importamos la librería
import tweepy

#definimos las variables que nos identifican junto con nuestra app
api_key = 'tus valores'
api_key_secret = 'tus valores'
access_token = 'tus valores'
access_token_secret = 'tus valores'

bearer_token = 'tus valores'

#creamos un cliente tweepy
cliente = tweepy.Client(bearer_token=bearer_token,
consumer_key=api_key,
consumer_secret=api_key_secret,
access_token=access_token,
access_token_secret=access_token_secret)

#llamamos a la query de twitter para publicarlo
cliente.create_tweet(text='Hola a todos!')

Y ya debería tener el tuit en el timeline.

Si, como es mi caso, quiere publicar el tuit con un gráfico se deberá subir previamente ese gráfico con el API v1, recoger el id, y añadir ese media_id en la llamada a la query. Queda el código tal que así : 

#importamos la librería
import tweepy

#definimos las variables que nos identifican junto con nuestra app
api_key = 'tus valores'
api_key_secret = 'tus valores'
access_token = 'tus valores'
access_token_secret = 'tus valores'
bearer_token = 'tus valores'

#hacemos una llamada al apiv1 para subir el gráfico
auth = tweepy.OAuth1UserHandler(api_key, api_key_secret)
auth.set_access_token(access_token, access_token_secret)
api = tweepy.API(auth)
media = api.media_upload(filename='media_horaria.png')
media_id = media.media_id

#creamos un cliente tweepy
cliente = tweepy.Client(bearer_token=bearer_token,
consumer_key=api_key,
consumer_secret=api_key_secret,
access_token=access_token,
access_token_secret=access_token_secret)

#hacemos la llamada para publicar, pero en esta ocasión con media
cliente.create_tweet(text='otra prueba, pero esta vez con gráfico',media_ids=[media_id])

Próximos pasos

Me he quedado con dos acciones :

  • No usar una librería externa y hacer llamadas directamente al API de twitter
  • Buscar un modo de subir el fichero con la v2 y no con la v1. Sospecho que en cualquier momento pueden meter alguna nueva limitación a la v1, y tener que rehacer los scripts de nuevo
  • ..y una tercera : tengo que añadir logs a los scripts para que me alerten si ha habido algún problema. Y así evitar estos 10 días sin publicar nada

Gracias a todos por los comentarios en twitter y los ánimos para seguir con estas tareas.

Descarga de datos del mercado eléctrico.

Manuel H. AriasDeja un comentario

Jugar con los datos abiertos que se proporcionan en las diferentes fuentes de información de este mercado es una buena manera de intentar entenderlo. En mi cuenta de twitter publico diariamente gráficos generados con datos descargados desde estas fuentes. Es un mercado ciertamente complejo, con una regulación extensa, y con mucho ruido mediático. Todo esto facilita la opacidad y dificultad de entender este mercado, que por otra parte se lleva, y más con la subida de precios de estos tiempos, una parte material del presupuesto de servicios básicos de las familias. Mi intención, publicando estas líneas de código (por otra parte extremadamente simple) es ayudar un poco en hacerlo más transparente.

¿Como lo he organizado?

He preparado un notebook de Jupyter mostrando una serie de funciones, en Python, para facilitar la descarga de datos desde fuentes relacionadas con el mercado eléctrico:

He preparado cinco funciones:

  • catalogo_esios(token): que permite bajar el catálogo completo de la api de esios, para, posteriorment, buscar de manera fácil los identificadores que necesitamos para nuestro trabajo
  • download_esios : que permite bajar datos de cualquier indentificador, entre dos fechas determinadas, para posteriormente trabajar sobre ellos.
  • download_ree : idem que el caso anterir pero sobre apidatos de REE
  • download_gas : que nos permite bajar desde https://mibgas.es el precio de gas GDAES del día siguiente
  • downlaod_gas_rd: que nos permite bajar desde https://mibgas.es el precio de gas correspondiente al mecanismo de compensación del RD10/2022

A modo de caso práctico, he añadido un ejemplo de descarga de datos junto con un gráfico para mostrarlos visualmente. He procurado elegir tipos diferentes de gráficos para cada gráfico por si es de ayuda.

Aquí pueden encontrar el notebook.

Me alegraré mucho si alguien lo encuentra de utilidad…

Mercamadrid

Manuel H. AriasDeja un comentario

Hemos preparado un código para bajar datos de la actividad comercial de mayoristas en Mercamadrid. Estos datos se pueden bajar desde este link del portal de datos abiertos del Ayuntamiento de Madrid.

La información esta estructura en una serie de campos tales como:

  • Fecha inicial del segmento de tiempo al que se refieren los datos
  • Fecha final del segmento de tiempo al que se refieren los datos
  • Descripción de la mercancia
  • Código de la mercancia
  • Origen de la mercancia
  • Código de este origen
  • Peso de la mercancia en Kilos
  • Precio mínimo registrado
  • Precio máximo registrado
  • Precio más frecuente

He intentado gestionar y minimizar el tamaño del pandas con el modelo propuesto por Matt Harrison, estoy haciendo un esfuerzo para seguir el «chaining» siempre que sea posible.

Presentamos el código necesario para bajar y preparar adecuadamente la información desde su repositorio en datos Madrid, y preparamos una rejilla de datos con los mismos..
En cada subgráfica, una por cada producto, presentamos la evolución del consumo como barras (eje «y» izquierda) )y la evolución de precios (eje «y» derecha). Para claridad se han codificado las barras según temperatura del mes..