Introducción al Dataframe de Pandas con Python (I)

En esta entrada vamos a trabajar con Pandas, una estructura de datos fundamental para trabajar organizar los datasets en DataScience. Es una libreria muy completa, muy documentada en multitud de blogs y que veremos como nos facilita el trabajo. Empecemos!:

import pandas as pd
import numpy as np

Leer más »

  

  

Análisis de la planta de Taxis de Madrid

Vamos a analizar el fichero de «Taxis»del Ayuntamiento de Madrid, con información sacada del portal de OpenData : https://datos.madrid.es/portal/site/egob/menuitem.c05c1f754a33a9fbe4b2e4b284f1a5a0/?vgnextoid=4f16216612d39410VgnVCM2000000c205a0aRCRD&vgnextchannel=374512b9ace9f310VgnVCM100000171f5a0aRCRD

Como siempre importamos las librerias necesarias : pandas, numpy, matplotlib,datetime..y añadimos calendar. Usaremos esta última para sacar el literal de un mes según su nº de orden.

import pandas as pd

import numpy as np

import matplotlib

import matplotlib.pyplot as plt

import datetime

import matplotlib.dates as mdates

%matplotlib inline

import matplotlib.ticker as mtick

from matplotlib.ticker import FuncFormatter
from mpl_toolkits.mplot3d import Axes3D

import calendar

pd.options.display.float_format = '{:,.1f}'.format

Preparamos una texto para incluirlo en cada gráfico como fuente…

fuente='Fuente : Ayuntamiento de Madrid, http://datos.madrid.es'

Construimos la URL de la fuente de datos :

path_web='https://datos.madrid.es/egob/catalogo/300219-0-taxi-flota.csv'

Leemos los datos desde su localizacion en ‘path_web’, en este fichero tenemos los datos de Junio de 2018.

taxis=pd.read_csv(path_web,sep=";",encoding='windows-1250',index_col=False)

Vemos unos ejemplos de lineas para asegurar que todo ha ido bien. Podemos chequear también las columnas

len(taxis)

15652

taxis.describe()

Index([‘Código’, ‘Matrícula’, ‘Fecha Matriculación’, ‘Marca’, ‘Modelo’, ‘Tipo’,
‘Variante’, ‘Clasificación medioambiental’, ‘Combustible’, ‘Cilindrada’,
‘Potencia’, ‘Número de Plazas’,
‘Fecha inicio de prestación del servicio de taxi’, ‘Eurotaxi’,
‘Régimen Especial de Eurotaxi’,
‘Fecha inicio Régimen Especial Eurotaxi’,
‘Fecha fin Régimen Especial Eurotaxi’, ‘Fecha’],
dtype=’object’)

Nos aseguraremos de que la columna ‘Fecha Matriculacíon’ tiene el formato Datetime para trabajos posteriores, y la ordenamos a continuación

taxis['Fecha Matriculación']=pd.to_datetime(taxis['Fecha Matriculación'],format='%d/%m/%Y')

taxis=taxis.sort_values(['Fecha Matriculación'])

Busquemos el Taxi con la matrícula más antigua :

print ('Matricula {} de fecha {}'.format(taxis['Matrícula'].iloc[0],taxis['Fecha Matriculación'].iloc[0].strftime('%d/%m/%Y')))

Matricula 2239DTJ de fecha 13/12/2005

..y con la matrícula más moderna :

print ('Matricula {} de fecha {}'.format(taxis['Matrícula'].iloc[-1],taxis['Fecha Matriculación'].iloc[-1].strftime('%d/%m/%Y')))

Matricula 8333KLS de fecha 12/06/2018

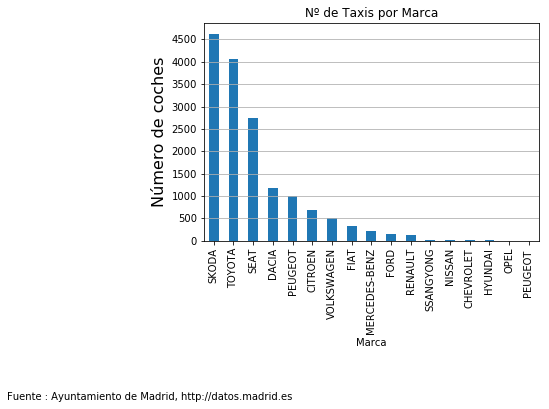
Calculemos la lista de número de Taxis por Marca

fig = plt.figure(1, (6,4))
ax = fig.add_subplot(1,1,1)
ax=taxis['Marca'].value_counts().plot.bar()
ax.locator_params(axis='y',nbins=10)
ax.set_xlabel('Marca')
ax.set_ylabel('Número de coches',size=16)
ax.grid(axis='y')
ax.set_title('Nº de Taxis por Marca')
fig.suptitle(fuente,size=10,x=0,y=-.4)
fig.savefig('Taxis por Marca',bbox_inches = 'tight')

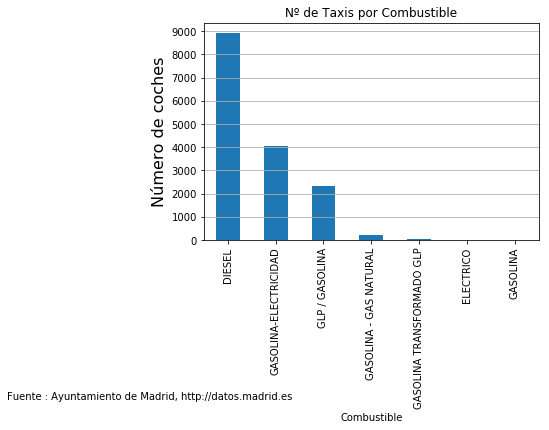
..ahora ordenaremos por combustible usado

fig = plt.figure(1, (6,4))
ax = fig.add_subplot(1,1,1)
ax=taxis['Combustible'].value_counts().plot.bar()
ax.locator_params(axis='y',nbins=10)
ax.set_xlabel('Combustible')
ax.set_ylabel('Número de coches',size=16)
ax.grid(axis='y')
ax.set_title('Nº de Taxis por Combustible')
fig.suptitle(fuente,size=10,x=0,y=-.4)
fig.savefig('Taxis por Marca',bbox_inches = 'tight')

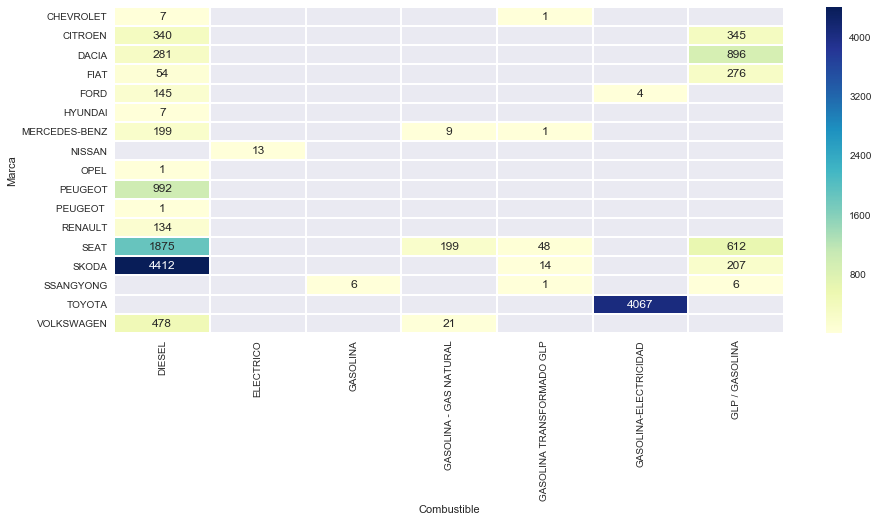
Ahora trabajemos estos dos últimos campos de manera conjunta. Empezamos con un ‘groupby’ por estos dos campos, añadiendo ‘size()’ para que nos calcule el tamaño de cada campo :

tabla=taxis.groupby([taxis['Marca'],taxis['Combustible']]).size()

tabla

Marca Combustible
CHEVROLET DIESEL 7
GASOLINA TRANSFORMADO GLP 1
CITROEN DIESEL 340
GLP / GASOLINA 345
DACIA DIESEL 281
GLP / GASOLINA 896
FIAT DIESEL 54
GLP / GASOLINA 276
FORD DIESEL 145
GASOLINA-ELECTRICIDAD 4
HYUNDAI DIESEL 7
MERCEDES-BENZ DIESEL 199
GASOLINA – GAS NATURAL 9
GASOLINA TRANSFORMADO GLP 1
NISSAN ELECTRICO 13
OPEL DIESEL 1
PEUGEOT DIESEL 992
PEUGEOT DIESEL 1
RENAULT DIESEL 134
SEAT DIESEL 1875
GASOLINA – GAS NATURAL 199
GASOLINA TRANSFORMADO GLP 48
GLP / GASOLINA 612
SKODA DIESEL 4412
GASOLINA TRANSFORMADO GLP 14
GLP / GASOLINA 207
SSANGYONG GASOLINA 6
GASOLINA TRANSFORMADO GLP 1
GLP / GASOLINA 6
TOYOTA GASOLINA-ELECTRICIDAD 4067
VOLKSWAGEN DIESEL 478
GASOLINA – GAS NATURAL 21
dtype: int64

Ya tenemos la tabla lista, ahora vamos a representarla. He encontrado este modelo de mapa de temperatura de SeaBorn que queda muy bien :

tabla=tabla.reset_index()
import seaborn as sns
sns.set()
matriz=tabla.pivot('Marca','Combustible',0)
f, ax = plt.subplots(figsize=(15, 6))
sns.heatmap(matriz, fmt=".0f", annot=True,linewidths=1, ax=ax, cmap="YlGnBu")

Insertemos ahora una columna con la antigüedad de cada Matricula, simplemente calculando la diferencia entre ‘ahora’ y la fecha de matriculación, que vendrá en días (.days) y la pasamos a años equivalentes dividiendo por 365 (nos olvidamos de los bisiestos!)

ahora=datetime.datetime.today()
taxis['antiguedad']=taxis['Fecha Matriculación'].apply(lambda x : (ahora-x).days/365)

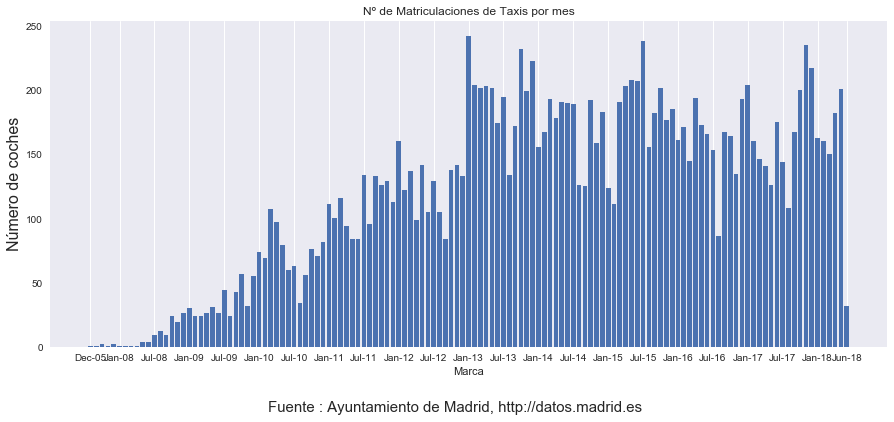
A continuación representamos una gráfica con el nº de matriculaciones ordenadas por meses :

fig = plt.figure(1, (15,6))
ax = fig.add_subplot(1,1,1)

data_series=taxis.groupby([taxis['Fecha Matriculación'].dt.year,taxis['Fecha Matriculación'].dt.month]).size()

ax.set_xlabel('Marca')
ax.set_ylabel('Número de coches',size=16)

ax.grid(axis='y')
ax.set_title('Nº de Matriculaciones de Taxis por mes')

bar_width=0.8
opacity=1
error_config = {'ecolor': '0.3'}
rects1 = ax.bar(np.arange(len(data_series.index.tolist())), data_series.values,bar_width,alpha=opacity)
def format_func(value, tick_number):
anno,mes=data_series.index.tolist()[int(value)]
mes=calendar.month_abbr[mes]
return mes+'-'+str(anno)[-2:]

ax.xaxis.set_major_formatter(plt.FuncFormatter(format_func))

# Preparamos una lista con los tickts que nos interesan : el primero, el último y todos los meses Enero y Julio
lista_ticks=[]
lista_ticks=[i for i in np.arange(3,len(data_series.index.tolist())) if data_series.index[i][1] in (1,7)]
lista_ticks.extend([0,len(data_series)-1]) #añade el primero y el último
ax.xaxis.set_ticks(lista_ticks)
fig.suptitle(fuente,size=15,x=0.5,y=0)
fig.savefig('matriculas por mes',bbox_inches = 'tight')
plt.show()

Utilicemos el campo ‘antiguedad’ para un par de cálculos y para generar una gráfica :

'Antiguedad media del parque de taxis : {:.1f} años, con desviación +/-{:.1f} años'.format(taxis['antiguedad'].mean(),taxis['antiguedad'].std())

‘Antiguedad media del parque de taxis : 4.0 años, con desviación +/-2.4 años’

Se nos ocurre generar una gráfica con la antigüedad media por Marca :

taxis.groupby(['Marca'])['antiguedad'].describe().sort_values(by='mean',ascending=False)

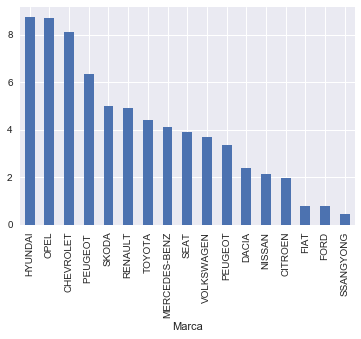
Y jugando un poco con Seaborn hemos encontrado este formato de gráficas que muestra muy claramente la contribución de cada generación de coches a esas medias :

sns.set(style="whitegrid", palette="muted")
n_de_marcas=8
#filtramos a las primeras n_marcas por volumen
#datos=taxis.loc[taxis['Marca'].isin(taxis_marca[:n_de_marcas].index)]
lista_topn_marcas=taxis['Marca'].value_counts().index[:n_de_marcas]
datos=taxis.loc[taxis['Marca'].isin(lista_topn_marcas)]
# Draw a categorical scatterplot to show each observation
f, ax = plt.subplots(figsize=(15, 6))
sns.swarmplot(x="Marca", y="antiguedad", ax=ax, data=datos)

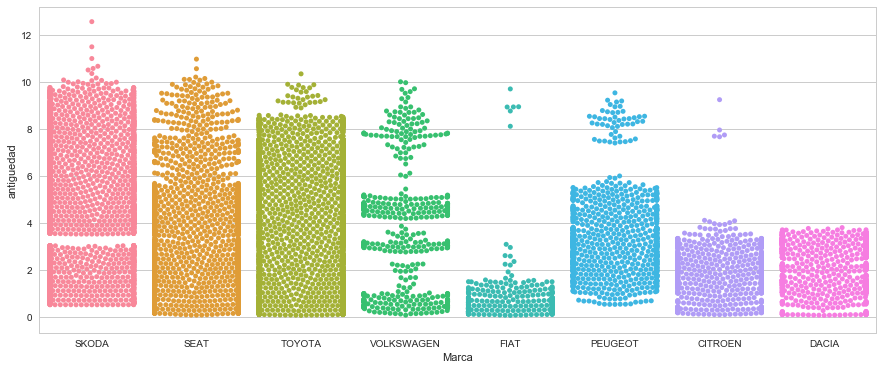
Vemos que se ha dejado de vender Skodas. Hay varios huecos en Volkswagen. Fiat ha empezado a vender en los dos últimos años. Peugeot ha dejado de vender también, y Dacia ha recupeado tras algún mes sin vender.

sns.set(style="whitegrid", palette="muted")
n_de_marcas=2
#filtramos a las primeras n_marcas por volumen
#datos=taxis.loc[taxis['Marca'].isin(taxis_marca[:n_de_marcas].index)]
lista_topn_marcas=taxis['Marca'].value_counts().index[:n_de_marcas]
datos=taxis.loc[taxis['Marca'].isin(lista_topn_marcas)]
# Draw a categorical scatterplot to show each observation

f, ax = plt.subplots(figsize=(15, 6))

sns.swarmplot(x="Marca", y="antiguedad",hue='Modelo', ax=ax, data=datos)
#lg=sns.legend_
plt.legend(ncol=2, loc='upper left')

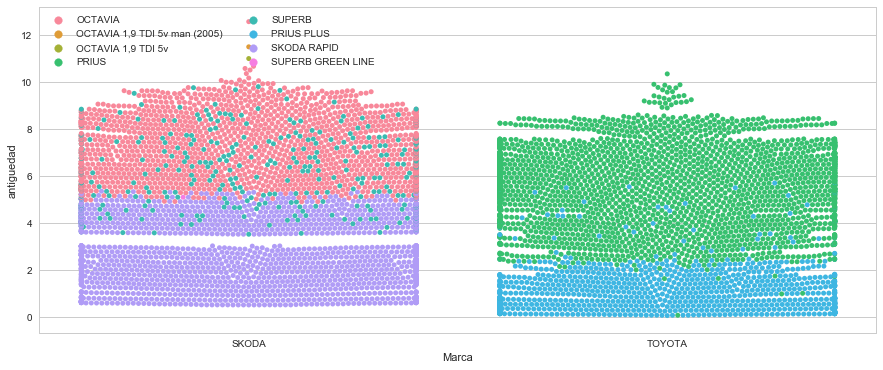
Eso es todo!

Problema del Análisis médico

Una determinada prueba clínica para detectar una enfermedad tiene una sensibilidad del 98%, es decir : en el caso de personas afectadas acierta en el 98% de los casos. El el 2% restante da resultado negativo, cuando debería de ser positivo (Falso Negativo).
Y tiene una especificidad del 99.0%, es decir : en el caso de personas sanas acierta en el 99.0% de los casos, y yerra en el 1.0% restante, dando un resultado positivo cuando en realidad el paciente está sano (Falso Positivo). La tasa de enfermos en la población del 0.5%.
La pregunta es : si hacemos un análisis a una persona elegida al azar de entre toda la población, y el resultado da positivo : ¿qué posibilidades hay de que realmente esté enferma?

Solución

La teoria de Bayes dice :

Vamos a aplicarlo con la siguientes nomenclatura:
: posibilidad de que el análisis de positivo
: posibilidad de que el análisis de negativo
: la persona está enferma
: la persona está sana

Aplicando los datos que nos han pasado en el enunciado :

El dato que nos piden es : probabilidad de que esté enfermo () habiendo dado positivo en el análisis ()

desarrollando el $\sum$ :

Usemos Python para el cálculo:

Empecemos importando una serie de librerías estandares en estas entradas :

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import re
import math

Criterio : mayúscula es positiva, minúscula es negativa

pAE=0.98
paE=1-pAE
pAe=0.01
pae=1-pAe
pE=0.005
pe=1-pE

pEA=pAE*pE/(pAE*pE+pAe*pe)

'La probabilidad de que esté enfermo dando positivo en el test es del {:1.2f}%'.format(100*pEA)

'La probabilidad de que esté enfermo dando positivo en el test es del 33.00%'

Esa es la razón por la que no tienen sentido análisis a la población en general cuando la tasa de afectados es muy baja.

Para entender el resultado hagamos una extrapolación para España (nº aprox)
Población : 46,5 millones, que podemos dividir en :

poblacion=46500000
poblacion_e=poblacion*pe
poblacion_E=poblacion-poblacion_e

'Poblacion afectada {:,.0f}'.format(poblacion_E)

'Poblacion afectada 232,500'

'Poblacion NO afectada {:,.0f}'.format(poblacion_e)

'Poblacion NO afectada 46,267,500'

aplicando p(A|e) a la poblacion no enferma nos encontrariamos con :

poblacionAe=poblacion_e*pAe

poblacionAe

462675.0

'es decir : tendriamos {:,.0f} False Positivos'.format(poblacionAe)

'es decir : tendriamos 462,675 False Positivos'

Y si hacemos el test solo a la poblacion afectada : cuantos positivos (verdaderos en este caso) tendriamos?

poblacionAE=poblacion_E*pAE

'{:,.0f} True Positivos'.format(poblacionAE)

'227,850 True Positivos'

Es decir : tenemos un total de positivos (los True y los False) de :

'{:,.0f} Positivos'.format(poblacionAE+poblacionAe)

'690,525 Positivos'

entre los que son True :

'True positivos {:,.0f} de un total de {:,.0f}, representando un {:2.1f}%'.format(
    poblacionAE,poblacionAE+poblacionAe,
100*poblacionAE/(poblacionAE+poblacionAe))

'True positivos 227,850 de un total de 690,525, representando un 33.0%'

que coincide con el resultado calculado anteriormente